The Great Central Sun of the Universe : Mechanika falowa Schrödingera i kopenhaska interpretacja funkcji Ψ

NIEWIARYGODNE! Świat otrzymał „szczegółowy obraz” wnętrza atomu, który widzimy, jako dziwne twory, nazwane orbitalami, otaczające jądro. Jak do tego doszło?

W 1909 roku A. Einstein

stwierdził, że światło ma dwoistą naturę i że może wykazywać zarówno właściwości fal, jak i również cząstek. Pomysł wydawał się nowatorski, ale został niby potwierdzfony eksperymentami.

Johannes Stark w 1909 r. napisał Einsteinowi wzór na pęd kwantu światła w postaci:

p=hν/c

A. Einstein posługiwał się tym wzorem dla cząstek światła, poruszających się z prędkością światła c i posiadających częstość ν.

Wzór Starka-Einsteina p = h/ λ ;

uzyskuje się poprzez przyrównanie wzorów:

E = m*c^2 oraz E = h*ν

E = m*c^2 = h*ν ; m*c*c = h/λ ; p*c = h/λ ; p = h/λc ; p = hν/c

c = λ/T = λν ; c/ ν = λ

a więc p = h/ λ

Dualistyczna hipoteza Einsteina stała się inspiracją dla historyka z wykształcenia, Louisa de Broglie'a,

który w 1923 roku zaczął się zastanawiać, czy sama materia nie ma właściwości zarazem cząstek i fal.
W 1924 roku, w swojej pracy doktorskiej, uogólnia teorię fotonową efektu fotoelektrycznego i wysuwa hipotezę fal materii, stwierdzając, że każda cząsteczka oprócz swej natury korpuskularnej posiada także naturę falową.

Propozycja de Broglie'a polegała na zwykłym odwróceniu rozumowania, aby każdej cząstce o różnym od zera pędzie przypisać falę, o określonej długości i częstotliwości. Zgodnie z tym, de Broglie zaproponował odwrócenie zależności między pędem a długością fali, znanej dla fotonu, tak, aby długość fali była wyrażona przez pęd cząstki.

Hipoteza ta nie miała żadnych podstaw doświadczalnych i była pozbawioną logiki spekulacją.

Louis de Broglie mówi:

Z każdym ciałem o pędzie p związana jest fala materii o długości λ danej wzorem:

λ = h/p

Wielu twierdzi, że jest to jego wzór de Broglie’a. Zastosowany przez niego do cząstek, ale A. Einstein posługiwał się tym wzorem

p = h/ λ

dla cząstek światła, poruszających się z prędkością światła c i posiadających częstość ν. Cząstki materialne natomiast nie poruszają się z tą prędkością światła c i nie mają własnej częstotliwości ν, jak kwanty światła, a więc wzór ten nie może być zastosowany do cząstek materialnych.

Ale historyk z wykształcenia de Broglie na bazie tej zależności

p = h/ λ

po prostym przekształceniu jej do postaci

λ = h/p

stworzył "podwaliny" pod tzw. teorię nowych kwantów. Jak daleko świat fizyki zauroczył się spekulacją de Broglie’a, możemy się przekonać, w wymienionym już wcześniej, Berkeley'owskim Kursie Fizyki, E.H. Wichman, Fizyka kwantowa, gdzie na str. 210, czytamy: Możemy, więc uwierzyć, że w odpowiednich warunkach doświadczalnych wielki fortepian będzie również zachowywał się jak fala.

Wcześniej się tam przyznaje, że cząstka o masie 10^-5 g (10 mikrograma) poruszająca się z prędkością 1 m/s miałaby długość około 6, 6*10^(-22) cm, co jest wielkością śmiesznie małą. A co dopiero fortepian o masie około 80 kg, jaką miałby długość fali de Broglie’a.

I to są te absurdy, które dostrzegam. Wzór Einstein wyprowadzony dla fotonów, zastosowany do fortepianu!!!

Reasumując: Nie można mechanicznie, by nie powiedzieć bezmyślnie, zastosować do cząstek materialnych takich jak elektron, wzoru Starka-Einsteina, bo nam wyjdą dziwne rzeczy.

p = h/λ

Jest to wzór, który stosował Einstein, dla fotonów a to jest zupełnie inna sprawa.

Schrodinger, jako pierwszy, uległ urokowi hipotezy de Broglie'a i zaczął "na własną rękę" poszukiwać dynamicznego równania, z którego mógłby wyznaczać własności fal materii.

Oczywiście, cały swój wywód, oparł na hipotezie de Broglie’a, że z każdym ciałem o pędzie p i prędkości V < c, związana jest fala materii o długości λ dana wzorem:

p = h/λ

W 1926 r. Schrodinger opublikował cztery artykuły pod wspólnym tytułem Quantisierung als Eigenwertproblem (tzn. Kwantowanie jako problem wartości własnych), przedstawiając metodę znajdowania dozwolonych stanów i energii układu fizycznego.
Pokazał, że jego równanie opisuje kwantowe reguły, rządzące atomem wodoru Bohra.

Oryginalne równanie Schrödingera ma postać:

Rozwiązanie tego równania "daje", dla różnych możliwych wartości energii E( E₁, E₂, E₃, ... E_n.), odpowiadające im stany własne funkcji Ψ(r) jako dyskretny zbiór rozwiązań.
Schrodinger interpretował w swoim równaniu funkcję falową Ψ(x) jako cząstkę, a w przypadku atomu wodoru, jako „elektron rozmyty w przestrzeni”.
Na taką interpretację nie dali jednak przyzwolenia ówcześni fizycy reprezentujący tzw. szkołę kopenhaską. Wzięli sprawę w swoje ręce, wyłączyli Schrodingera z gry, unieważnili jego interpretacje i dorobili swoją. Orzekli, że funkcja falowa będąca rozwiązaniem równania jest funkcją o wartościach zespolonych. Z tego powodu, nie jest oczywista jej interpretacja fizyczna.
Poza tym, co najważniejsze, równanie daje dyskretny zbiór rozwiązań i stany własne, zwane stanami stacjonarnymi, które nie reprezentują rzeczywistości.

Niemiecki fizyk Max Born

w roku 1926 podał interpretację, która stała się standardową interpretacją: kwadrat modułu funkcji falowej

jest gęstością prawdopodobieństwa znalezienia cząstki (układu) w określonym położeniu, w określonym czasie. I dalej, poprawne rozwiązanie to funkcja

zcałkowana po całym obszarze.

Ta interpretacja Maxa Borna została uznana za "dobrą" przez fizyków kopenhaskich. I choć jest obowiązuje do dzisiaj.
Schrodinger był zdruzgotany, że jego „ukochana dyskretna teoria falowa” poległa, zmieniona na gęstość prawdopodobieństwa, przez Maxa Borna.

Heisenberg w liście do Pauliego podsumował to następująco, pisząc :

„Im więcej myślę o części fizycznej teorii Schrodingera, tym bardziej obrzydliwa mi się ona wydaje."
Schrodinger próbując ratować swoją interpretację, w 1935 roku, opublikował w trzech częściach artykuł przeglądowy: „Obecna sytuacja w mechanice kwantowej”,

[1] [PDF]E. Schrödinger. Die gegenwärtige Situation in der Quantenmechanik[1]
THE PRESENT SITUATION IN QUANTUM MECHANICS: A TRANSLATION OF SCHRÖDINGER'S "CAT PARADOX PAPER"

w którym ukazał istotę swej falowej mechaniki kwantowej w kontekście absurdalnej interpretacji kopenhaskiej i sporu EPR. Schroedinger w tym przeglądowym artykule: „Obecna sytuacja w mechanice kwantowej”, tłumaczy m. inn: splątanie kwantowe.

Jeżeli mamy układ dwóch co najmniej obiektów kwantowych (cząstek lub fotonów), to musimy równanie tak ustawić, by funkcja falowa Ψ opisywała cały układ, a nie każdy składnik z osobna. Będzie ona funkcją wielu zmiennych położeniowych i będzie ewoluować w czasie jednolitym dla wszystkich cząstek.

I wystarczy, że jedna cząstka zmieni swój stan, a wszystkie pozostałe muszą natychmiast zmienić swoje stany kwantowe, gdyż rządzi nimi taka sama, jedna funkcja falowa.

Schröedinger natychmiast wyraził swoje zdumienie i zaniepokojenie, że z formalizmu matematycznego utworzonego przez niego, dla opisania zachowania kwantowych obiektów, wynikają dwa paskudne fakty:

1. wzajemny wpływ obiektów tworzących układ kwantowy, nie zależy od odległości między nimi

2. wpływ ten jest natychmiastowy, czyli oddziaływanie wzajemne (jeśli takowe jest) rozprzestrzeniało się z nieskończenie wielką prędkością.

Te dwa hipotetyczne fakty zadecydowały o tym, że Schroedinger ubolewał nad tym, iż los tak zrządził, że to on był odkrywcą tak irracjonalnego zachowania się przyrody, a Einstein umarł z głębokim przeświadczeniem, że mechanika kwantowa jest niezupełną teorią mikroświata, i zawiera wg niego ukryty, nieusuwalny defekt logiczny. I tak to jest na tym świecie, wg Schrödingera.
Schrödinger interpretował w swoim równaniu funkcję falową Ψ(x) jako „cząstkę rozmazaną w przestrzeni”.

Natomiast interpretacja kopenhaska interpretowała wg kwadratu prawdopodobieństwa i obserwacjach. Absurdalność tej kopenhaskiej interpretacji, przedstawił to na przykładzie zamkniętego pudła z atomem radioaktywnego pierwiastka, fiolki z trucizną, detektora promieniowania, urządzenia, które uwalnia truciznę w momencie, gdy detektor zarejestruje rozpad atomu oraz, co ciekawe, żywego kota.

jednocześnie żywy i martwy kot kopenhaski

Wg interpretacji kopenhaskiej, atom bowiem znajduje się w superpozycji stanów „przed rozpadem” i „ po rozpadzie”.
Dopóki nie podejrzymy atomu, jeżeli nie wykonamy pomiaru, nie dowiemy się, w jakim stanie on istnieje. Atom wybierze ostatecznie dopiero swój stan dopiero pod wpływem pomiarów.
Jeżeli wypiszemy funkcję falową dla układu złożonego z atomu i kota, to musimy stwierdzić, że zanim wykonamy pomiar (np. zajrzymy do pudła) kot znajduje się w superpozycji stanów kota żywego i kota martwego:

Dopiero pomiar powoduje redukcję wektora stanu: jeżeli zajrzymy do pudła, to zaobserwujemy kota żywego albo kota martwego z prawdopodobieństwem ½.

Wg tzw. kopenhaskiej mechaniki "kwantowej", do momentu przeprowadzenia pomiaru, tzn. stwierdzenia, co dzieje się z kotem, jego stan jest fundamentalnie nieokreślony, kot znajduje się w stanie superpozycji, czyli jednocześnie w każdym możliwym stanie, a więc jest jednocześnie i żywy i martwy.
Fizycy kopenhascy mówią o superponowanym stanie żywego i martwego kota.

Dopiero otwarcie pudła powoduje tzw. załamanie funkcji falowej i kot jednoznacznie przyjmuje jeden stan. A mówiąc ogólnie, dopiero pomiar rozstrzygnie jego stan.

Tak narodził się jednocześnie żywy i martwy kot Schrödingera, choć tak naprawdę to powinien nazywać się kot kopenhaski, gdyż to tzw. szkoła kopenhaska, na czele z Bohrem, Heisenbergiem i Borem, stworzyła filozofie indeterminizmu, a w powyższym przypadku wykreowała, do momentu pomiaru, jednocześnie żywego i martwego kota. I tak to jest na tym świecie, wg kopenhaskiej mechaniki "kwantowej".

Przewidywania szkoły kopenhaskiej, wydają się, trzeźwo myślącym ludziom, dość osobliwe, by nie powiedzieć dziwaczne a pojęciowo „oszałamiające”. Wprowadziły one w fizyce kwantów wiele zamieszania i nieporozumienia, zamiast je wyjaśnić.

Rozkład radialny R(r) i rozkład prawdopodobieństwa radialnego P(r) dla najniżej leżących stanów w atomie wodoru.

Zauważamy, że R_n0 ma w r = 0 maksimum! Jednak czynnik r² redukuje w tym miejscu prawdopodobieństwo do zera. Tym niemniej, jak przyznają sami fizycy, jest niezerowa możliwość, że elektron jest wewnątrz jądra.

Jednak, gdy się przejdzie na prawdopodobieństwo radialne, po scałkowaniu

, to w tym miejscu redukuje np. to max R(r) = R₁₀do zera i P₁₀_,jako max pojawia się na ... promieniu Bohra r = a₀.
Jednym słowy, funkcje gęstości prawdopodobieństwa - P(r)_n, w sposób zasadniczy, różnią się od funkcji własnych - R(r)_n, (dyskretny zbiór rozwiązań).

Wykres prawdopodobieństwa radialnego P_r = R_nl^*R_nldV_r w zależności od odległości r wyrażonej w jednostkach promienia Bohra r = 5,3*10^-11 m

Na powyższym rysunku żółty kolor stanu p, powinien być oczywiście, koloru zielonego. Widzimy, że:

W stanie 1s – p(r), żółty kolor, jest maksymalne dla r = r₁ = 5,3*10^-11 m, co, o dziwo, zgadza się z wartością promienia orbity elektronu dla stanu podstawowego atomu, obliczonej na podstawie teorii Bohra.

W stanie 2s (n = 2, l = 0) – p(r), oczywiście zielony kolor, górny wykres ma dwa maksima; jedno dla r = r₁, a drugie dla r = 5r₁, przy czym drugie maksimum jest wyższe niż pierwsze.

W stanie 2p (n = 2 ,l = 1) – p(r), zielony kolor zamiast żółtego, środkowy wykres, osiąga maksimum w pobliżu r = 5r₁.

W stanie 3s (n = 3, l = 0) – p(r), niebieski kolor, górny wykres ma trzy maksima: r₁, 4r₁ oraz 12r₁, przy czym ostatnie z nich jest najwyższe.
W stanie 3p (n=3, l=1) – p(r), niebieski kolor, środkowy wykres, osiąga maksimum w pobliżu r ≈3r₁ i r ≈12 r₁

W stanie 3d (n=3, l=2) – p(r), niebieski kolor, dolny wykres, osiąga maksimum w pobliżu r ≈10 r₁

Mamy podwójne a nawet potrójne maxima. Jest to dziwne i niezrozumiałe. Kompletna bzdura. Wg mnie, dyskwalifikuje to całą metodę.

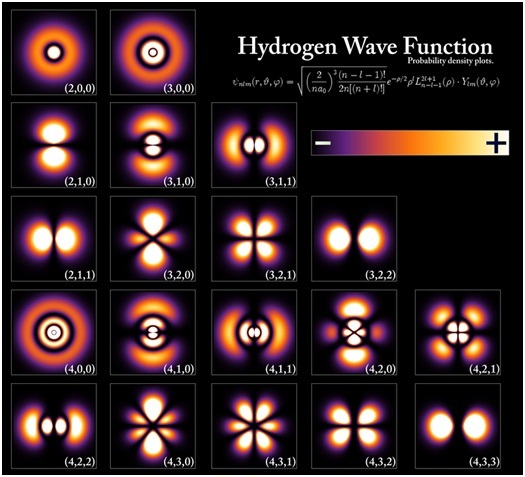
Popatrzmy, jak wg kopenhaskiej mechaniki "kwantowej", na poszczególnych poziomach kwantowych, wygląda atom wodoru:

NIEWIARYGODNE!

Świat otrzymał „szczegółowy obraz” wnętrza atomu, który widzimy, jako dziwne twory, nazwane orbitalami, otaczające jądro.
Czy takie "równania" Schrodingera można więc poważnie traktować? Wg mnie, nie.

Oryginalnego wyprowadzenie powyższego wzoru Schrödinger nie zostawił po sobie. Pytanie dlaczego? Ano dlatego, że tak można wiele ukryć i nie tłumaczyć się. Ale można dojść, jak on doszedł do swego wzoru i wtedy fałsz widać, jak na dłoni. Gdzie więc leży błąd? Poważny błąd leży w założeniach a subtelny w pozornie logicznym wyprowadzeniu podstawowego równania. Budowa wyjściowego równania energii zbyt ogólna, no i dalej te urojone fantazje falowe. I czy z takiego równania z wszczepionymi mu urojonymi fantazjami falowymi , może wyjść coś dobrego? Tylko urojenie. Rozumne stosowanie liczb zespolonych jest zawsze dobre ale zawsze pozostaje problem ich interpretacji fizycznej. Schrodinger się bawi nimi, jak małe dziecko zapałkami, no i wyszedł mu z tego dym.
Fizycy reprezentujący tzw. szkołę kopenhaską postanowili na swój sposób usunąć ten dym, wzięli sprawę w swoje ręce, wyłączyli Schrodingera z gry, unieważnili jego interpretacje i dorobili swoją. Orzekli, że interpretacja fizyczna funkcji falowej będącej rozwiązania równania, jako funkcji o wartościach zespolonych, nie jest oczywista. Zaproponowali: kwadrat modułu funkcji falowej

jako gęstością prawdopodobieństwa znalezienia cząstki (układu) w określonym położeniu, w określonym czasie. Ta interpretacja została uznana za "dobrą" przez fizyków kopenhaskich. Schrodinger był zdruzgotany, że jego „ukochana dyskretna teoria falowa” poległa, zmieniona na gęstość prawdopodobieństwa, przez Maxa Borna.

Stan fizyki pierwszej połowy XX w. w jakimś stopniu oddają trzy poniższe wypowiedzi wielkich i uznanych fizyków:

Albert Einstein: „Zachowuję się jak struś, który cały czas chowa głowę w piasek względności, aby nie patrzeć w twarz wstrętnym kwantom.” a na starość: „Pięćdziesiąt lat dociekań, nie doprowadziło mnie bliżej do odpowiedzi na pytanie, czym właściwie są kwanty światła.”

Wolfgang Pauli: „…Fizyka jest dla mnie zbyt trudna i żałuję, że nie zostałem komikiem filmowym lub kimś w tym rodzaju, aby nigdy nie słyszeć więcej o fizyce”.

Antoon Lorentz: „Straciłem przekonanie, że moja praca naukowa prowadziła do obiektywnej prawdy, i nie wiem, po co żyłem: żałuję tylko, że nie umarłem pięć lat wcześniej, gdy jeszcze wszystko wydawało mi się jasne”.
Erwin Schrodinger: „Jeśli te wszystkie przeskoki kwantowe miałyby pozostać, to powinienem być zmartwiony, to powinienem być zmartwiony, że kiedykolwiek związałem się z teorią kwantów".

A dzisiejsi fizycy, uznając autorytet Fizyki mówią, że fizyka kwantowa jest magiczna:

„W pierwszej połowie dwudziestego wieku nasze wyobrażenie o Wszechświecie zostało wywrócone do góry nogami. Stare, klasyczne teorie fizyczne zastąpił nowy sposób postrzegania świata - mechanika kwantowa. To odmienne widzenie świata pod wieloma względami nie zgadza się z koncepcjami starszej, newtonowskiej mechaniki; prawdę powiedziawszy, w wielu wypadkach jest ono sprzeczne ze zdrowym rozsądkiem. Jednakże najdziwniejszą cechą tych nowych teorii jest niezwykła zgodność ich przewidywań z obserwowanym zachowaniem układów fizycznych. Niezależnie od tego, jak bardzo zwariowana może się czasami wydawać mechanika kwantowa, Natura najwyraźniej chce, aby tak właśnie było - i musimy się z tym pogodzić. Zachowanie ciał według mechaniki kwantowej wydaje się nie przystawać do naszego sposobu myślenia i staje się łatwiejsze do zaakceptowania poprzez analogie do sytuacji, które znamy, nawet jeśli te analogie są niezbyt dokładne. Takie porównania nigdy w pełni nie odzwierciedlają rzeczywistości, ponieważ zjawiska kwantowe są naprawdę zupełnie odmienne od naszych codziennych doświadczeń”.

W 1928 roku Dirac (mając niecale 24 lata), dokonał uogólnienia równania Schrödingera, doprowadzając do stworzenia relatywistycznej teorii elektronu.

Ponadto równanie Diraca "wyjaśniało" właściwości elektronu.
Jest ono podstawowym równaniem w relatywistycznej mechanice kwantowej. Równanie Schrödingera, jak wiemy, ma postać:

Równanie Diraca można przekształcić do analogicznej postaci wprowadzając macierze:

Wtedy równanie Diraca przyjmie postać:

Przy czym

jest operatorem Hamiltona.

W zapisie relatywistycznie niezmienniczym równanie Diraca dla cząstki swobodnej ma postać:

gdzie:

- współrzędne punktu w czasoprzestrzeni

- czterogradient

Jako, że energia w rozwiązaniu ma postać jej kwadratu,

E² = m₀²c⁴ + p²c²

to pierwiastki z tego równania są dwa:

"Król QM" - Dirac stwierdza, że jego równanie opisujące falę elektronową ma dwa rozwiązania, z czego płyną doprawdy dziwaczne konsekwencje: powinna istnieć inna cząstka o własnościach identycznych z elektronem, różniąca się od niego tylko ładunkiem elektrycznym. Stoi za tym bardzo proste matematyczne pojęcie: każde dziecko wie, że pierwiastek kwadratowy z 4 równy jest 2 oraz –2, bo 2 × 2 = 4 i –2 × –2 = 4. Istnieją, więc dwa rozwiązania: plus albo minus dwa. Ale też, każde dziecko ze szkoły wie, że ujemny pierwiastek nie ma sensu fizycznego i jest odrzucany.

Ale dla Diraca „symetria” wynikająca z jego „równania” oznaczała, iż dla każdej cząstki musi istnieć inna cząstka o takiej samej masie i przeciwnym ładunku elektrycznym.

Dirac, będąc konserwatywnym i przyziemnym dżentelmenem, stwierdził, iż w przyrodzie obok ujemnych cząstek muszą występować także dodatnie.

Wymyślił więc, w roku 1930, swój model próżni, jako nieskończonego morza cząstek posiadających negatywną energię. Dziurę w morzu elektronów utożsamiał z protonem.

Ktoś ukuł termin antymateria. Ta antymateria miała znajdować się wszędzie dookoła, tylko jakoś nikt nigdy jej jeszcze do tej pory nie zauważył.

Los dał, że z pomocą przyszedł mu młody fizyk z Caltech, Carl Anderson, który w 1932r. złapał w swojej mgłowej komorze jedną dziwaczną nową cząstkę, a właściwie jej ślad. Nazwał ten nowy obiekt pozytonem, bo był, podobny do elektronu, tylko, że zamiast ujemnego, miał dodatni ładunek. Uznano, że Anderson znalazł nową postać materii, antycząstkę, która parę lat wcześniej wyskoczyła z równania Diraca i jest to cząstka przybywająca z odległego zakątka naszej Galaktyki, czy może nawet jakiejś „AntyGalaktyki”. Ale, dla mnie, nie jest to jakaś tajemnicza antymateria z niewiadomo skąd. Promieniowanie gamma, jak wiemy, ma naturę elektromagnetyczną, elektron, bardziej elektryczną a ta, jak się wyrażono, dziwaczna, nowa cząstka, pozyton- naturę bardziej magnetyczną. Z tego powodu, można a nawet lepiej, by tę cząstkę nazwać, w przeciwieństwie do elektronu, zwykłym magnetronem. A teorię o antymaterii, cząstek przybywających z odległych zakątków naszej Galaktyki, włóżmy między bajki.

P.Dirac hołdował idei fix, piękna teorii jako kryterium. Niby ładnie to brzmi, bo przecież Natura jest zawsze piekna. Zaczął mówiać, jak poniżej:

Teoria fizyczna musi posiadać matematyczne piękno

Paul Dirac, 1956

Ale swoim oponentom, tym, którzy nie uznawali jego teorii, już “konkretniej” mówił:

“Ten wynik jest zbyt piękny, aby być fałszywym; ważniejsze jest, aby uzyskać

piękne równania, niż aby pasowały one do eksperymentu”

Paul Dirac, 1963, “The evolution of the Physicist's Picture of Nature” Scientific

American 208 (5)

Powstrzymam się od komentarza. Jaki koń jest widać. Ot, cały Dirac.

Z „równania” Diraca wychodzi pelna symetria (to “piękno” które miało nobilitować jego teorię), a więc powinno być tyle samo jednych i drugich; natomiast w otaczającej nas rzeczywistości …

Antymateria we wszechświecie

Z bezpośrednich obserwacji wiadomo, że cały układ słoneczny i jego najbliższe otoczenie zbudowane są ze zwykłej materii. Analiza pierwotnego promieniowania kosmicznego pokazuje, że jest to prawdą również dla odleglejszych obiektów. W zakresie energii pomiędzy 1 - 50 GeV antyprotony stanowią mniej niż 0,01% docierających do Ziemi cząstek pierwotnego promieniowania kosmicznego, a ich liczba i rozkład energii są zgodne z obliczeniami przeprowadzonymi przy założeniu, że są one cząstkami wtórnymi, produktami zderzeń pierwotnego promieniowania z cząsteczkami gazu międzygwiazdowego. Wynika stąd, że całe pierwotne promieniowanie kosmiczne w zakresie średnich energii składa się z materii, co wskazuje, że obiekty je emitujące również są zbudowane z materii.

Pośrednim argumentem za tym, że cały obserwowany wszechświat jest zbudowany ze zwykłej materii, są negatywne próby zaobserwowania promieniowania powstającego podczas anihilacji materii i antymaterii. Gdyby we wszechświecie istniały duże skupiska antymaterii, musiałyby też istnieć obszary graniczne, gdzie materia wyrzucona z galaktyk spotykałaby się z antymaterią wyrzuconą z „antygalaktyk”, dochodziłoby do anihilacji i uwolnienia znacznych energii w postaci promieniowania o charakterystycznych energiach. Promieniowania takiego jednak nie zaobserwowano, co świadczy, że widzialna część wszechświata nie zawiera znaczących obszarów zbudowanych z antymaterii.
Pogląd o istnieniu w całym Wszechświecie tylko materii oparty jest też na obserwacjach rozpadu mezonów K0. Okazuje się, że antymaterialny odpowiednik K0 rozpada się o 7 przypadków na 1000 rzadziej niż K0.

I tak to jest, gdy się bezmyślnie interpretuje napisane przez siebie równania.

Poniżej najmądrzejsi ówczesnego świata fizyki:

Fifth conference participants, 1927. Institut International de Physique Solvay in Leopold Park.

We thought you would enjoy this remarkable image of the October 1927 Fifth Solvay International Conference on Electrons and Photons. It was at this conference that the world’s most notable physicists met to discuss the then brand-new quantum theory. The leading figures at the conference were Nobel Prize winners Albert Einstein and Niels Bohr. Einstein, disenchanted with Heisenberg’s “Uncertainty Principle,” was said to have remarked “God does not play dice,” to which Bohr then replied, “Einstein, stop telling God what to do.”

Back Row: A. Piccard, E. Henriot, P. Ehrenfest, Ed. Herzen, Th. De Donder, E. Schrödinger, J.E. Verschaffelt, W. Pauli, W. Heisenberg, R.H. Fowler, L. Brillouin;
Middle Row: P. Debye, M. Knudsen, W.L. Bragg, H.A. Kramers, P.A.M. Dirac, A.H. Compton, L. de Broglie, M. Born, N. Bohr;
Front Row: I. Langmuir, M. Planck, M. Curie, H.A. Lorentz, A. Einstein, P. Langevin, Ch. E. Guye, C.T.R. Wilson, O.W. Richardson

Tzw. „nowa” teoria kwantowa, zwana mechaniką kwantową, ma, co najmniej, dwie godne podkreślenia własności, by nie powiedzieć, wady:

po pierwsze, jest sprzeczna ze zdrowym rozsądkiem,
po drugie, pewne jej aspekty sprawiły, że Einstein, Schrödinger i im podobni nie potrafili jej zaakceptować i z tego powodu wciąż jest przedmiotem wytężonych badań.

A więc:

Są z nią pewne problemy. Chodzi o funkcję falową Ψ i o to, co ona oznacza. Mimo że „nowa” teoria kwantowa odniosła pewne sukcesy, nie możemy być całkowicie pewni, co ona oznacza. Niektórzy mówią, że nasze zakłopotanie w obliczu „nowej” teorii kwantowej, jest skutkiem konstrukcji psychicznej ludzkiego umysłu, ale możliwe także, że pojawi się jeszcze kiedyś jakiś geniusz, który opracuje schemat pojęciowy zadowalający wszystkich.

Jeśli „nowa” teoria kwantowa przyprawia cię o mdłości, nie martw się: jesteś w doborowym towarzystwie. Wielu fizyków, każdy oczywiście na swój sposób, nie mogło się z nią pogodzić, między innymi Planck, Einstein, de Broglie i Schrödinger. Richard P. Feynman powiedział: Myślę, że mogę śmiało powiedzieć, że nikt nie rozumie mechaniki kwantowej.

Istnieje bogata literatura na temat zastrzeżeń wobec propabilistycznej natury teorii kwantowej. Bohr dobrze zaczął z kwantami w atomie wodoru, ale później stał się orędownikiem najbardziej egzotycznych idei mechaniki kwantowej, czyli zjawiska dualizmu korpuskularno - falowego oraz zasady nieoznaczoności.
Einstein przewodził walce z Bohrem i podjął długą serię usilnych prób podważenia tejże zasady nieoznaczoności.

Bohr stworzył to, co dziś zwiemy „kopenhaską interpretacją” mechaniki kwantowej. Bohr i Einstein przyłożyli się do dyskusji.
Einstein konstruował eksperymenty myślowe, które miały zadać cios w samo serce nowej teorii kwantowej, a Bohr, zazwyczaj po całym weekendzie ciężkiej pracy, wynajdywał błąd w jego rozumowaniu.
W sporze tym Einstein odgrywał rolę kłopotliwego dzieciaka (jak ten, który na lekcjach religii pyta: Jeśli Bóg jest wszechmocny, to czy może stworzyć tak wielki kamień, że go sam nie może podnieść?) i wciąż wymyślał nowe paradoksy ukryte w teorii kwantowej. Bohr, niczym ksiądz, wciąż obalał wysuwane przez Einsteina obiekcje.

By zdemaskować niekompletność tej koncepcji toru-widma, Einstein zaproponował pewien eksperyment. Eksperyment ten został opisany we wspólnie wydanej w 1935 roku publikacji "Can Quantum Mechanical Description of Physical Reality Be Considered Complete?". Jest on znany, jako eksperyment myślowy EPR – od nazwisk trzech jego twórców: Einstein, Podolsky i Rosen.

Einstein wiedział, że z założeń tej nowej mechaniki kwantowej wynika "dziwne oddziaływanie na odległość", gdzie szybkość ruchu cząsteczek bądź przekazywania informacji przekracza prędkość światła. Sam był zwolennikiem realizmu lokalnego - zakładającym, że parametry cząstek kwantowych mają wartości niezależne od aktów obserwacji i że oddziaływania fizyczne zachodzą ze skończoną prędkością.
Einstein postanowił strzelić w kopenhaską interpretację fizyki kwantowej z ich własnej broni i zaproponował myślowe doświadczenie z udziałem dwóch cząstek, których losy są ze sobą ściśle związane. Fizycy twierdzą, że znają metody tworzenia par cząstek w ten sposób, że mogą mieć przeciwne spiny: jeśli jedna z nich wiruje w dół, to druga musi wirować w górę, albo jedna w lewo, a druga w prawo. Wysyłają jedną cząstkę na Marsa, a drugą na Wenus. Einstein powiedział: w porządku, zaakceptujmy fakt, że nie wiemy nic o cząstce aż do chwili pomiaru. Mierzymy, więc cząstkę A na Marsie i stwierdzamy, że ma spin skierowany w prawo. Wiemy teraz coś o cząstce B, znajdującej się na Wenus, której jeszcze nawet nie poddano obserwacjom. Na początku cząstka mogła z prawdopodobieństwem równym 0,5 mieć spin skierowany zarówno w prawo, jak i w lewo. Teraz, po pomiarze dokonanym na Marsie, wiemy, że cząstka na Wenus wiruje w lewo. Ale skąd ona, na Wenus, wie, w jakim stanie jest ta na Marsie ? Fale świetlne podróżują potrzebują trochę czasu na przebycie od cząstki A do cząstki B. Co to za system komunikowania się, by nie poruszać się szybciej od światła? Einstein nazywał to zjawisko „upiornym oddziaływaniem na odległość”.

Kopenhagczycy odpowiedzieli, że związek między zdarzeniami dotyczącymi cząstki A (decyzja wykonania pomiaru A) a rezultatem pomiaru B można zrozumieć tylko pod warunkiem, że dysponuje się dodatkowymi danymi, a teoria kwantowa nie może ich dostarczyć.

Aha! – zawołał Albert. – Mechanika kwantowa jest niekompletna!

Kiedy Einstein przyłożył Bohrowi tym eksperymentem, ruch uliczny w Kopenhadze zamarł, a Bohr zagłębił się w rozważaniach. Einstein próbował podejść z boku zasadę nieoznaczoności Heisenberga, dokonując pomiaru towarzyszącej cząstki. Bohr w końcu odpowiedział, że nie można separować zdarzeń dotyczących A i B, że układ musi obejmować zarówno A, jak i B oraz obserwatora, który decyduje, kiedy dokonywać pomiarów. Sedno problemu tkwi w tym, czy cząstka A i obserwator (albo detektor tej cząstki) istnieje rzeczywiście, czy też przed pomiarem są tylko nic nieznaczącymi, tymczasowymi duchami.

W roku 1936 Einstein stwierdził, że mechanika kwantowa nie może być kompletnym opisem świata, nawet, jeśli pozwala określić prawdopodobieństwo wyników rozmaitych pomiarów.

Bohr odpowiedział, że niekompletność, która tak frasowała Einsteina, nie jest brakiem teorii, tylko własnością świata, w którym żyjemy.

Zasada Heisenberga mówi: żadne wysiłki zmierzające do jednoczesnego ustalenia, gdzie cząstka jest i dokąd się udaje, nie mogą nigdy zostać uwieńczone całkowitym sukcesem. „Nowa” teoria kwantowa mówi, że droga do końca jest niepoznawalna. Wszystkie drogi są możliwe, każda z pewnym prawdopodobieństwem.

Einstein uznawał, że świat w gruncie rzeczy zbudowany jest w sposób klasyczny i relatywistyczny, a obowiązująca w mechanice kwantowej zasada nieoznaczoności Heisenberga jedynie tymczasowo ogranicza nasze poznanie. Einstein był gorącym zwolennikiem teorii ukrytych zmiennych, pojmując istnienie cząstek w sposób klasyczny i nie zgadzając się z propabilistyczną interpretacją funkcji falowych. Twierdził, że cząstka tak naprawdę posiada pęd i położenie w sensie klasycznym, natomiast niemożliwość ich jednoczesnego ustalenia wynikająca z zasady nieoznaczoności może minąć, gdy mechanikę kwantową zastąpi nowsza teoria, "uchylająca" nieoznaczoność. Takiemu postawieniu sprawy przez Einsteina sprzeciwiał się, jak już powiedzieliśmy, Niels Bohr i cała szkoła kopenhaska, która interpretowała mechanikę kwantową, jako mechanikę falową.

Albert Einstein należał do jej największych krytyków kopenhaskiej szkoły mechaniki kwantowej. Nie uznawał przewidywanej przez nią losowości zdarzeń (mawiał: "Bóg nie gra w kości) i wierzył, że w przyszłości powstanie teoria, która tą losowość wyeliminuje. W liście do Maxa Borna z 1944 r. pisał:

„Znaleźliśmy się na antypodach w naszych naukowych oczekiwaniach. Ty wierzysz w Boga, który gra w kości, a ja w całkowity porządek i prawo, obowiązujące w obiektywnie istniejącym świecie; próbuję je, w szalenie spekulatywny sposób, uchwycić. Mocno wierzę, ale mam nadzieję, że ktoś odkryje bardziej realistyczny sposób czy raczej bardziej namacalną podstawę, niż mnie przypadła w udziale. Nawet wielkie początkowe sukcesy teorii kwantowej nie skłoniły mnie do uwierzenia w leżącą u podstaw grę w kości, chociaż doskonale zdaję sobie sprawę, że nasi młodsi koledzy interpretują to, jako oznakę mej starości. Nie ulega wątpliwości, że nadejdzie dzień, który rozstrzygnie, czyje przeczucia były prawdziwe.”

Albert Einstein na koniec powiedział:
„Zachowuję się jak struś, który cały czas chowa głowę w piasek względności, aby nie patrzeć w twarz tym wstrętnym kwantom.”

E. Schrödinger (1926): "Quantisierung als Eigenwertproblem (Erste Mitteilung)". Annalen der Physik 79, 361-376.