Bo odpowiedzi na trudne pytania fizyki leżą, nie we względności, nie w poruszających się z prędkością światła układach, ale raczej w bezwzględności m. inn.w Słońcu, w świetle, w atomie,etc.; jednym słowem w Naturze. Przedstawiam tutaj takie moje refleksje na jej temat m. inn: na tle wspominków A. Einsteina rozumienia fizyki światła z lat jego młodości i stworzenia przez niego teorii względności.
Albert Einstein, Autobiographisches
A. Einstein: z paradoksu, na który się natknąłem, gdy miałem 16 lat, po 10 latach rozmyślań taka zasada zrodziła mi się: Jeżeli podążę za promieniem światła z prędkością c, to taki promień powinienem widzieć jako pole elektromagnetyczne w spoczynku, ale oscylujące w przestrzeni. Wydaje się jednak, że coś takiego nie może istnieć, co wynika zarówno z doświadczenia, jak i również z równań Maxwella.
Einstein leci z prędkością światła c, widzi czoło, front i mówi, że: „powinienem widzieć jako pole elektromagnetyczne w spoczynku” ... ale zaraz się poprawia i mówi: wydaje się jednak, że coś takiego nie może istnieć a w dalszym ciągu światło pędzi przed nim ze prędkością c.
Einstein ma kompleks prędkości światła.
Nie chce zrozumieć, że światło porusza się w eterze i jego prędkość względem eteru jest zawsze stała.
Albert Einstein - ether and electromagnetic fields
Wg niego prędkość światła jest stała, ale nie względem eteru ale obserwatora.
Albert Einstein - spacetime relativity theory
dalej A.Einstein mówi: Od samego początku wydawało mi się intuicyjnie jasne, że z punktu widzenia takiego obserwatora wszystko musi się dziać zgodnie z tymi samymi prawami, co dla obserwatora pozostającego w spoczynku względem Ziemi.
Einstein może sobie wyobrazić, że leci z prędkością światła, ale nie może sobie wyobrazić, że wtedy światło powinien widzieć w spoczynku ale widzi, że ono w dalszym ciągu pędzi ono przed nim ze prędkością c.
Jest to zdumiewające myślenie.
I jeszcze Einstein pyta: W jaki bowiem sposób obserwator mógłby wiedzieć lub stwierdzić, że jest w szybkim ruchu jednostajnym?
Powtórzmy
jego, Einsteina, pytanie: W jaki
bowiem sposób pierwszy obserwator mógłby wiedzieć lub stwierdzić,
że jest w szybkim ruchu jednostajnym?
Jak
nie wie, no to po prostu nie wie, bo to nie zawsze można stwierdzić.
Ale, jak można, no to stwierdzamy i już. W wielu przypadkach
rozumem możemy pomóc naszym zmysłom i to stwierdzić. Na
siłę mówić, że nie wiem, jak mogę wiedzieć, jest dziwne.
Wszyscy np. piloci statków muszą nieraz do wskazań przyrządów
czy nawet własnych zmysłów angażować swój rozum, by stwierdzić
jak się poruszają np. patrząc na gwiazdy, używając kompasu,
żyroskopu, patrząc na napęd pojazdu etc. Ale Einstein,
ciągle 16-letni, mówi: nie wiem, czy stoję, czy lecę.
Kiedyś myślano, że Słońce krąży wokół Ziemi. Rozum człowieka nie wiedział, że jest odwrotnie. Nucono, więc piosneczkę: Zachodź, że Słoneczko, skoro masz zachodzić, bo nas nogi bolą po tym polu chodzić. Ale dzisiaj wiemy, że to Ziemia krąży wokół Słońca. Są metody by się dowiedzieć czy stoimy, czy lecimy.
I tu jest einsteinowskie błędne myślenie.
To,
że my, ludzie, nie czujemy, gdy poruszamy się jednostajnie, to nie
znaczy, że się nie poruszamy.
Einstein jest naiwny jak małe
dziecko siedzące w pociągu na stacji, który wolno jedzie. Sam tego
kiedyś, będąc małym chłopcem doświadczyłem. Mój pociąg wolno
jechał i ja odnosząc się do dworca wiedziałem, że jadę.
Nagle
nadjechał z boku drugi pociąg i mi nagle zaczęło się wydawać,
że on jedzie a ja stoję.
I mi to pasowało. Ale też sobie
sytuację za chwile odwróciłem, że ja jadę a on stoi i też mi to
pasowało. Ale nie dałem się nabrać jak 16-letni Albert;
wiedziałem bowiem, że prawda jest tylko jedna a drugi wariant to
złudzenie.
Wniosek: To, co my czujemy nie jest wiarygodne, innymi
słowy nie jest prawdą, bo to jest subiektywne odczucie na bazie
naszych kiepskich zmysłów i przy ruchu jednostajnym. Do naszych
zmysłów należy dołączyć rozum. A.
Enstein nie dołączył rozumu.
Twierdzi
on, że możemy przyjąć, że my stoimy, skoro nie czujemy a nie
czujemy bo jedziemy jednostajnie. I przyjmujemy, że światło
porusza się względem nas z prędkością c. Chłopiec w tamtym
pociągu też nie czuje, że jedzie, bo to ruch też jednostajny i
też do swoich spekulacji ze światłem przyjmuje, że prędkość
światła względem niego jest c. Do swych zmysłów nie dołącza
rozumu.
Taka zabawa - każdy „pali
głupa”, że nie wie czy jedzie czy
stoi, a więc zakłada dla uproszczenia, że stoi i każde światło
rozchodzi się względem niego z prędkością c. I na tym polega
istota teorii względności Einsteina.
A.Einstein: „Widzimy,
że paradoks ten zawiera już zarodek szczególnej teorii
względności. Dziś każdy oczywiście wie, że wszelkie próby
wyjaśnienia tego paradoksu były skazane na niepowodzenie dopóki w
naszej podświadomości tkwi aksjomat o absolutnym charakterze
czasu.
Właściwie już rozpoznanie tego aksjomatu i jego
arbitralnego charakteru zawiera o w sobie zasadnicze elementy
rozwiązania problemu...”
Wielki
Czarodziej Albert nawet nas usprawiedliwia, mówiąc, że: w naszej
podświadomości tkwi aksjomat o absolutnym charakterze czasu.
I,
dlatego:
wszelkie próby wyjaśnienia
tego paradoksu były skazane na niepowodzenie.
Tak,
nasza podświadomość jest ułomna, bo może mięliśmy trudne
dzieciństwo i tych jego mądrych, choć prostych rzeczy nie
rozumiemy.
I jakie konsekwencje takiego einsteinowskiego
myślenia.
Jak na dłoni widać błędność
założeń tej jego teorii.
I wyszło
z tego krzywe zwierciadło, w którym, oczywiście można się
przeglądać, ale obraz jest zniekształcony i oczywiście w pobliżu
prędkości światła; natomiast w odległości od tej prędkości –
do przyjęcia.
I ludzie się na to „łapią”. Wielki
Czarodziej Albert ludzi zaczarował i oczarował swoim ograniczonym
myśleniem.
Dalej
Einstein pisze:
„Dobrze wiadomo, że
elektrodynamika Maxwella – jak się ją dziś rozumie – w
zastosowaniu do ciał w ruchu prowadzi do asymetrii, które nie
wydają się być nieodłączne od zjawisk.
Weźmy, na przykład,
oddziaływanie elektromagnetyczne między magnesem i przewodnikiem.
Obserwowane tu zjawisko zależy tylko od ruchu względnego
przewodnika i magnesu, podczas gdy zwyczajowe ujęcie wprowadza
wyraźne zróżnicowanie między dwoma przypadkami, w których jedno
lub drugie z tych ciał jest w ruchu.”
Jeśli natomiast magnes jest w spoczynku, a przewodnik w ruchu, w otoczeniu magnesu nie powstaje żadne pole elektryczne, natomiast w przewodniku pojawia się siła elektromotoryczna, której nie odpowiada żadna energia, lecz która prowadzi – przy założeniu równości ruchu względnego w obu dyskutowanych przypadkach – do powstania prądów elektrycznych o takim samym natężeniu i kierunku, jak te, które są wytwarzane przez siły elektryczne w pierwszym przypadku.”
To prawda, że opisy, równania matematyczno-fizykalne się różnią a mogłyby być jednakowe, ale tak to Faraday i inni opisali, chwała im za to i tak jest. Kto umie niech to poprawi.
I z tych jakby zrozumiałych uproszczeń dokonuje A. Einstein resume i wyrzuca ostatecznie karty na stół, mówiąc: „Podobne przykłady, jak również bezowocne próby wykrycia ruchu Ziemi względem „ośrodka światłonośnego”, prowadzą do założenia, że nie tylko zjawiska mechaniczne, lecz także elektrodynamiczne, nie mają właściwości odpowiadających pojęciu absolutnego spoczynku”.
A.Einstein: Należy raczej przypuszczać, że te same prawa elektrodynamiki i optyki są słuszne we wszystkich układach współrzędnych, w których obowiązują prawa mechaniki, co już zostało udowodnione dla wielkości pierwszego rzędu.”
I autorytatywnie już stwierdza podpierając się teorią Maxwella:
A.Einstein: „Temu przypuszczeniu, które będziemy dalej nazywali „zasadą względności”, nadamy rangę postulatu; ponadto wprowadzimy jeszcze jeden postulat, tylko pozornie sprzeczny z tym pierwszym, że światło w próżni rozchodzi się z określoną prędkością, która nie zależy od stanu ruchu ciała je wysyłającego.
Te dwa postulaty wystarczają do podania prostej, wolnej od sprzeczności elektrodynamiki ciał w ruchu, opartej na teorii Maxwella dla ciał spoczywających.”
I teraz coś miłego na uspokojenie, jak ktoś nie zrozumiał o co Wielkiemu Czarodziejowi Albertowi chodzi:
„Wprowadzenie „eteru światłonośnego”, okaże się zbyteczne, ponieważ w przedstawionych tu poglądach ani nie ma potrzeby „przestrzeni w absolutnym spoczynku” obdarzonej specjalnymi właściwościami, ani też potrzeby przypisywania wektora prędkości jakiemukolwiek punktowi pustej przestrzeni, w której zachodzą procesy elektromagnetyczne.
Teoria tu rozwijana, podobnie jak każda inna elektrodynamika, opiera się na kinematyce ciała sztywnego, ponieważ twierdzenia każdej teorii tego rodzaju dotyczą związków między ciałami sztywnymi (układami współrzędnych), zegarami i procesami elektromagnetycznymi. Niedostateczne uwzględnienie tej okoliczności jest źródłem trudności, z jakimi zmaga się obecnie elektrodynamika ciał w ruchu.”
Jaki on jest kochany i już nie chce zawracać nam głowy jakimś eterem, bo i po co. Usłyszmy to jeszcze raz:
Wprowadzenie „eteru światłonośnego”, okaże się zbyteczne, ponieważ w przedstawionych tu poglądach ani nie ma potrzeby „przestrzeni w absolutnym spoczynku” obdarzonej specjalnymi właściwościami, ….
No pewnie, po co wprowadzać „eter światłonośny” i robić sobie korowód i jeszcze tłumaczyć ludziom jak ten eter wygląda.
Ale w roku 1920 Wielki Czarodziej Albert zmienił swoje zdanie o eterze i powiedział:
„Bardziej szczegółowe rozważania uczą nas jednak, że szczególna zasada względności nie wymaga wyparcia się istnienia eteru.”
„Negowanie eteru prowadzi, bowiem do negowania jakichkolwiek własności fizycznych pustej przestrzeni. Taki pogląd jest jednak sprzeczny z podstawowymi faktami mechaniki.”
Błądzenie jest rzeczą ludzką.
A. Einstein: O tym, że pole magnetyczne jest wzbudzonym stanem eteru przekonuje nas istnienie stałych magnesów, gdyż zasada zachowania energii wyklucza w tym przypadku możliwość istnienia stanu ruchu.
Ruch eteru spowodowany prądem elektrycznym będzie trwał dopóki działające siły elektromotoryczne nie zostaną skompensowane siłami pasywnymi powstającymi w wyniku deformacji źródłem, których jest sam ruch eteru.
Wspaniałe doświadczenia Hertza genialnie naświetliły dynamiczną naturę tych zjawisk – rozchodzenie się w przestrzeni, a także jakościową tożsamość tych zjawisk ze światłem i z ciepłem.
Wierzę, że aby zrozumieć zjawiska elektromagnetyczne należy podjąć wszechstronne badania doświadczalne potencjalnych stanów eteru w różnego rodzaju polach magnetycznych.
Innymi słowy należy mierzyć deformacje elastyczne i działające siły odkształcające.
Nie ulega kwestii, iż doświadczenie Michelsona wywarło poważny wpływ na moją pracę w tym sensie, że wzmocniło moje przekonanie o słuszności zasad szczególnej teorii względności. Z drugiej zaś strony byłem dość mocno przekonany o słuszności tej zasady, nim dowiedziałem się o samym eksperymencie i jego wyniku. W każdym razie doświadczenie Michelsona rozwiało, praktycznie biorąc, wszelkie wątpliwości, jeśli chodzi o słuszność tej zasady w optyce, i wykazało, że zasadnicza zmiana podstawowych pojęć fizyki jest nieunikniona.
Sam Michelson w swojej książce Studies in Optics opublikowanej w 1927 r. stwierdził, że teoria względności musi zostać zaakceptowana przez wszystkich, chociaż początkowo nie należał do jej gorących entuzjastów.
http://www.archive.org/stream/mathphyspapers01stokrich#page/n151/mode...
G. Stokes pisze wyraźnie, że Ziemia i planety niosą ze sobą część eteru.
Tą częścią jest cały dysk Układu Słonecznego.
Do następnej Gwiazdy jest kilka lat świetlnych. Między gwiazdami eter jest prawie nieruchomy.
W owym czasie każdy astronom już widział wszędzie dyski. Było oczywiste, co G. Stokes miał na myśli.
Ziemia nie unosi eteru, tak samo jak eter nie unosi Ziemi. Ziemia i eter razem ze sobie krążą.
Nie stwierdziło, bo nie mogło go stwierdzić. Obydwa ramiona interferometru M-M, były bowiem nieruchome względem eteru Ziemi, droga w obydwu ramionach była jednakowa a więc i czasy przelotu swiatła były jednakowe. I dlatego nic nie stwierdzono.
Ale Wielki Czarodziej Albert sobie myślał: niby interferometer M-M porusza się wraz z Ziemią wokół Słońca, jest emisja i rozdwojenie światła wzgledem obydwu ramion interferometru, ale skoro czasy przelotu światła w obydwu ramionach są jednakowe to przy tej samej predkości światła musza być takie same drogi przelotu, nie dochodzi więc do skrócenia drogi i możemy powiedzieć, że prędkość światła względem obydwu ramion interferometru M-M jest taka sama. A więc czy stoimy czy lecimy, prędkość światla względem nas jest zawsze stała. I to jest to fundamentalne założenie einsteinowskiej teorii względności.
Innymi słowy jest on pod wielkim wrażeniem prędkości światła i mu się wydaje, że wynosi ona nieskończoność. Gdyby była ona nieskończoność, to tak istotnie mogli byśmy myśleć i mówić.
Dla naszego życia codziennego i w naszych odczuciach oraz w większości zagadnień elektryczno-dynamicznych tak jest - można zaokrąglać prędkość światła c=3 000 000 km/s i przyjmować dla uproszczenia jego nieskończoność.
Ale jeśli chcemy naszymi wyprowadzonymi wzorami na bazie zaokrąglenia prędkości światła do nieskończoności, później wprowadzić c=3 000 000 i analizować na podstawie tego wzoru co się dzieje w pobliżu prędkości światła no to oglądamy rzeczywistość niczym w krzywym zwierciadle, bo nam tam w pobliżu c wszystko „puchnie”.
Masy dążą do nieskończoności, pręty się dziwnie wydłużają a bliźniaki nie równo się starzeją – jednym słowem wszystko się „wygina” i „przegina”. Tak, Wielki Albert, jak mówi młodzież, przegina. Oj, zdrowo przegina!
I takie wykombinowane przez niego krzywe zwierciadło nadaje się tylko do kabiny śmiechu.
Kiedyś, jak byłem mały, to w takiej kabinie śmiechu nawet byłem i widziałem się i miałem tam bardzo duży nos i długie uszy.
I było to takie nawet wesołe i do śmiechu. Ale przeglądać się można i każdy siebie nawet rozpoznawał.
Położenie i czas wyznaczone przez obserwatora w tym układzie oznaczone jest symbolami
x, y, z, t
Jeśli źródło światła znajduje się w początku układu S i emisja rozpoczyna się w chwili t=0, to równanie kulistego czoła fali będzie miało postać:
x2+y2+z2=c2t2
Równanie to opisuje falę kulistą, której promień wzrasta z prędkością światła c.
Położenie i czas mierzone przez obserwatora w tym układzie oznaczone jest symbolami ze znakiem prim:
x’, y’, z’, t’.
Dla wygody załóżmy, że dla
t=0
również
t’=0
oraz że w chwili początkowej początek układu
x’, y’, z’.
znajduje się w tym samym punkcie, co źródło światła w układzie S. Wtedy dla obserwatora w układzie S’ równanie kulistego czoła fali będzie miało postać:
x’2+y’2+z’2=c2t’2
A powinno być, wg mnie, c-V, bo źródło światła było założone na początku w spoczynku.
Załóżmy, że układ S’ porusza się w kierunku +x, ze stałą prędkością V względem układu S. Znana nam wszystkim transformacja Galileusza by wyglądała:
x’=x-Vt, y’=y, z’=z, t’=t.
Ale tutaj po podstawieniu otrzymuje się:
x2-2xVt+V2t2+y2+z2=c2t2
x’=x-Vt, y’=y, z’=z, t’=t+fx ,
gdzie f jest pewna stałą, która należy wyznaczyć.
Po podstawieniu otrzymuje się:
x2 - 2xVt + V2t2 + y2 + z2 = c2t2 + 2c2 ftx + c2 f2x2
Widać, że wyrazy zawierające xt znikają, jeśli założymy, że
f=-V/c2 , czyli t’=t-Vx/c2
wobec tego wyrażenie będzie miało postać.
x2[1-V2/c2]+y2+z2=c2t2[1-V2/c2]
Widzimy, że pojawił się „dziwny” czynnik
No i mamy tu powyżej te czarujące zwierciadełka, jako segmenty całego zwierciadła TW, które w pobliżu prędkości światła w naszych oczach, poprzez ten „dziwny” czynnik
Ale ludzie się cieszą, bo coś się dzieje a przecież o to w tym wszystkim chodzi.
A jeśli komuś coś nie pasuje, to Wielki Czarodziej Albert przypomina, że w naszej podświadomości tkwi aksjomat o absolutnym charakterze czasu … i dlatego nie przejmujmy się tym.
Wielki Albert, jak przystało na Wielkiego Czarodzieja, ujmuje to też czarująco i krótko:
Prędkość światła w próżni jest taka sama dla wszystkich obserwatorów, taka sama we wszystkich kierunkach i nie zależy od prędkości źródła światła.
W obydwu równaniach prędkość światła jest stała I wynosi c, a powinno być w układzie primowanym c-v bądź c+v w zależności od kierunku.
I dalej, już w OTW, jest liczona jeszcze nawet pochodna tego czterowektora położenia względem tego urojonego interwału czasoprzestrzennego ds i nazywa się to czterowektorem prędkości.
Tak się zastanawiam, jaki może być sens takiej pochodnej po tym urojonym ds?
Chyba też jakieś urojenie.
Do pełnego zrozumienia ogólnej teorii względności, potrzebna jest wyrafinowana i zawiła matematyka, a więc zostanie tu przedstawiony tylko sens fizyczny podstawowych idei i równań OTW.
- stałości prędkości światła względem wszystkich układów poruszających się ruchem jednostajnym oraz na
- zasadzie równoważności masy bezwładnej i grawitacyjnej
„Skonstruował” więc z tego swego powyższego wzorku swój tensor energii-pędu Tμν , który zawiera w sobie jako składowe zarówno energię własną (spoczynkową), jak i energie potencjalne, kinetyczne, strumienie pędu, ciśnienie w ośrodku ciągłym, energie naprężeń itp. i wstawił go zamiast gęstości masy na prawą stronę równania Poissona.
Einstein zdał sobie sprawę, że w teorii relatywistycznej, gdzie rządzi czasoprzestrzenny interwał:
Tensor metryczny
Odległość pomiędzy punktami wyznaczana jest przez tensor metryczny, który całkowicie determinuje krzywiznę przestrzeni.
Można zauważyć, że człony: Δx2, Δy2, Δz2 mnożone są przez 1, a człon c2Δt2 - przez -1, to tensor metryczny ημν będzie miał postać tablicy:
Jak widać, wszystkie współczynniki tego tensora są stałymi, więc przestrzeń układu inercjalnego jest płaska.
- Gdyby tensor po prawej stronie był zerowy (przestrzeń bez materii), to jego strona lewa również musiałaby mieć wszystkie składowe zerowe.A nie istnieją przestrzenie z tensorem metrycznym mającym same zerowe współczynniki, bo oznaczałoby to brak jakiejkolwiek odległości pomiędzy punktami.
- Skoro tensor metryczny determinuje krzywiznę, a tę ostatnią możemy utożsamiać z polem grawitacyjnym, to analogia z równaniem Poissona nakazuje szukać nie tyle tensora metrycznego, co tensora składającego się z drugich pochodnych tensora metrycznego po współrzędnych czasoprzestrzeni.
W powyższym wzorze, współrzędne: x, y, z i t są oznaczane przez: xσ, xμ, xβ i xν.
Tensor Riemanna mierzy krzywiznę w danym punkcie przestrzeni. Jeśli wszystkie jego składowe w danym punkcie są zerowe, to przestrzeń jest płaska, a jeśli nie - to ma ona krzywiznę.
Z tensorem krzywizny jest jednak inny problem. Ma on 4 indeksy: σ, μ, β i ν. Każdy z tych indeksów przyjmuje w czterowymiarowej czasoprzestrzeni niezależnie 4 wartości: 1,2,3 i 4. A więc mamy 4 x 4 x 4 x 4 = 44 = 256 składowych tego tensora, a to jest za dużo jak na lewą stronę szukanego równania.
Istnieje inny tensor, który jest wersją okrojoną tensora Riemanna. Jest to tensor Ricciego. Ma on 16 składowych z których każda zawiera następującą sumę składowych tensora Riemanna:
Po kilku nieudanych próbach Einstein znalazł w końcu tensor pokrewny tensorowi Ricciego, który ma znikającą dywergencję i zapostulował wreszcie formę swoich tensorowych równań pola, w których po lewej stronie umieścił obiekt zwany dziś tensorkiem Einsteina — w postaci:
a po prawej zaś tensor energii-pędu Tμν.
Ostateczna forma zapisanych przez Einsteina równań wiążących geometrię czasoprzestrzeni z rozkładem masy - energii i pędu, ma postać:
Dla słabych i stałych pól, powyższe równanie OTW powinno przechodzić w równanie Poissona. Ale czy przechodzi?
Ostatecznie równanie OTW, czyli równanie Einsteina, w pełnej „krasie” jest:
W rzeczywistości jest ich tylko 6, gdyż są one jeszcze dodatkowo powiązane tzw. tożsamościami Bianchiego.
Równanie Einsteina pozwala wyznaczyć tensor metryczny czasoprzestrzeni, mając dany rozkład materii-energii po prawej stronie. Jak już zostało powiedziane, tensor metryczny w pełni determinuje krzywiznę.
Ale obraz się komplikuje, gdy równanie tensorowe są rozpisywane na składowe. Otrzymuje się wówczas układ sześciu niezależnych równań różniczkowych w skondensowanej postaci. Każdy z członów jest skrótem wyrażenia bardziej skomplikowanego.
Derivation of the Einstein E=mc2
W 1905 r. ukazała się w „Annalen der Physik”, tom 18, krótka praca Einsteina zatytułowana: Czy bezwładność ciała zależy od jego energii? Ponizej przedstawienie tej pracy. W pracy tej Einstein założył, że światło to fale świetlne (lichtwallen) o energii E, której wartość jest proporcjonalna do częstotliwości promieniowania f .
Einstein dalej mówi: niech ciało spoczywające w układzie O, o początkowej energii E0, emituje w pewnej chwili dwie identyczne fale świetlne, o energii e/2 każda, w dwóch przeciwnych kierunkach (czyli łącznie emituje energię e). Ponieważ każda fala świetlna o energii e/2, unosi identyczny pęd, lecz o przeciwnym zwrocie, po emisji ciało będzie nadal spoczywać. Jeżeli energię całkowitą ciała po emisji oznaczymy Ek, to na podstawie zasady zachowania energii możemy zapisać:
Rozważa dalej to samo zjawisko w układzie O' poruszającym się względem O z prędkością v (wzdłuż osi równoległej do kierunku emisji fali świetlnej). Porcje energii emitowane przez ciało będą w tym układzie różne (wskutek relatywistycznego efektu Dopplera):
, ponieważ względem obserwatora O' źródło promieniowania znajduje się w ruchu. Ponieważ energia promieniowania jest proporcjonalna do częstotliwości, w układzie O' równanie zasady zachowania energii zapisuje następująco:
Następnie równania zapisane w dwóch układach odejmuje od siebie stronami.
Ponieważ w układzie O ciało spoczywa, jego energia jest energią spoczynkową E0. Względem układu O' ciała zarówno przed, jak i po emisji paczek energii porusza się z prędkością v, więc energia w tym układzie jest sumą energii spoczynkowej i kinetycznej, stąd E0' - E0 = Ekin 0, oraz Ek' - Ek = Ekin k. Przyjmując, że prędkość względna układów v jest dużo mniejsza od prędkości światła (b<<1) stosuje przybliżenie:
Ostatecznie otrzymuje:
Przyrównując do klasycznego wzoru na energię kinetyczną:
zauważa, że w wyniku emisji dwóch fal świetlnych o energii e/2 każda, nie zmieniła się prędkość ciała. Musiała więc ulec zmianie jego masa.
Wynika stąd: Einstein mówi o tym następująco: „ Jeśli ciało wysyła w postaci promieniowania, energię e, to jego masa zmniejsza się e/c2". Innymi słowy: fala świetlna (lichtwallen) posiada masę.OTW to układ sześciu niezależnych równań różniczkowych w skondensowanej postaci. Każdy z członów jest skrótem wyrażenia bardziej skomplikowanego. Ocenia się, że gdyby zapisać równania Einsteina bez żadnych skrótów, liczba członów byłaby rzędu ... dziesięciu tysięcy. Dlatego trzeba przyznać, że powyższy słynny wzór E= mc2, w przeciwieństwie do tasiemcowych i złożonych wzorów OTW, jest prosty i, jak by powiedział "Król QM" P. Dirac,
na pewno prawdziwy. P. Dirac hołdował bowiem idei fix, piękna teorii jako kryterium. Niby ładnie to brzmi, bo przecież Natura jest zawsze piękna. Zaczął mawiać: ”teoria fizyczna musi posiadać matematyczne piękno” ( Paul Dirac, 1956). Ale swoim oponentom, tym, którzy nie uznawali jego teorii, już mówił “konkretniej”: “Ten wynik jest zbyt piękny, aby być fałszywym; ważniejsze jest, aby uzyskać piękne równania, niż aby pasowały one do eksperymentu” (Paul Dirac, 1963, “The evolution of the Physicist's Picture of Nature” Scientific American 2008)
O okolicznościach towarzyszących temu zaćmieniu piszą Poor (1930), Brown (1967), Ciark (1984) i McCausIand (2001). To, co czyni ekspedycje do Sobral i Principe (2) tak podejrzanymi, to żarliwe poparcie, jakiego Eddington udzielił Einsteinowi, co widać w jego oświadczeniu: „Stojąc na stanowisku sprawdzania i ostatecznie weryfikując teorię , nasze narodowe obserwatorium podtrzymało najlepsze tradycje naukowe” (Ciark, 1984). W tym przypadku Eddington był wyraźnie na bakier z podstawowymi założeniami nauki.
Jego zadaniem było zbieranie danych a nie weryfikowanie teorii Einsteina.
Dalsze dowody oszustwa można wydedukować z osobistych oświadczeń Eddingtona przedstawionych przez Ciarka (Jak wyżej, str. 285): „29 maja od rana padał deszcz, który ustał dopiero około południa. Aż do 13.30, kiedy zaćmienie już się zaczęło, zespół nie uzyskał widoczności Słońca. Musieliśmy wykonać nasze fotografie na wiarę”. Z tego opisu widać wyraźnie prawdziwe nastawienie Eddingtona, który był zdeterminowany zrobić wszystko, aby udowodnić, że Einstein miał rację. Eddingtona nic nie było w stanie powstrzymać.
„Wyglądało na to, że wbrew ogromnemu wysiłkowi, przynajmniej w odniesieniu do ekspedycji na Principe, całość mogła okazać się fiaskiem”.
„Wywoływaliśmy zdjęcia, po dwa każdej nocy przez sześć nocy po zaćmieniu… Pochmurne niebo zniweczyło moje plany i musiałem potraktować pomiary w inny sposób, niż zamierzałem, i dlatego nie mogłem wystosować wstępnego doniesienia o wynikach” (Ciark, jak wyżej).
W rzeczywistości słowa Eddingtona mówią wszystko o wyniku.
Gdy tylko znalazł strzęp danych, które były w zgodzie z ogólną teorią względności „Einsteina”, natychmiast ogłosił to jako jej potwierdzenie.
Czy tak powinna wyglądać nauka?
Czy ktoś poza Eddingtonem rzucił okiem na te zdjęcia?
Otóż była taka osoba.
Człowiek ten nazywał się Poor i w całości odrzucił wyniki Eddingtona.
Powinno to zmusić do zastanowienia się każdego etycznego naukowca.
"Ani jedna z zasadniczych koncepcji zmienności czasu albo zwijania lub skręcania przestrzeni, jednoczesności lub względności ruchu nie jest w żaden sposób związana z przewidywaniami Einsteina dotyczącymi ugięcia światła ". "Wielu ekspedycjom związanym z zaćmieniami Słońca nadano fikcyjną rangę. Ich wyniki nie są w stanie udowodnić ani obalić teorii względności ..." (Poor, 1930).
To, na czym bazował, było przedwczesną oceną płytek fotograficznych. Początkowo światło gwiazd zdawało się uginać, tak jak powinno, jak wymagała tego teoria Einsteina, ale potem, jak twierdzi Brown, przyszło niespodziewane: światło kilku gwiazd uginało się w kierunku poprzecznym do spodziewanego, a jeszcze innych w kierunku przeciwnym, niż przewidywała teoria względności.
Dziwnym zbiegiem okoliczności 15 procent "dobrych" danych było zgodnych ze skalą stałej Einsteina.
Ostatecznie dane dotyczące gwiazd, które nie potwierdzały wniosków wypływających z teorii Einsteina, trafiły do szuflady i mit poszedł w świat, i z czasem uprawomocnił się.
Gdy pisał swój opublikowany w 1935 roku elaborat, z całą pewnością musiał znać pracę Poora, w której czytamy: "Rzeczywiste przesunięcia gwiazdowe, jeśli mają miejsce, w najmniejszym stopniu nie wykazują podobieństwa do przewidzianych przez Einsteina - nie są zgodne co do kierunku, rozmiarów ani stopnia spadku wraz z oddalaniem się od Słońca".
Dlaczego Einstein nie ustosunkował się do publikacji, która bezpośrednio godziła w jego pracę?
Dlaczego zwolennicy Einsteina nie starali się wyjaśnić sprawy fałszywych danych z roku 1919?
McCausIand (2001) cytuje byłego redaktora magazynu Naturę, Johna Maddoxa: "[Crommelin i Eddington] byli zdeterminowani dokonać pomiaru odchylenia promieni świetlnych..."
"Wbrew faktowi, że dowody eksperymentalne teorii względności z roku 1919 wydają się być bardzo liche, niesamowita sława Einsteina pozostała nietknięta, a jego teoria jest nadal traktowana jako jedno z największych osiągnięć ludzkiej myśli".
Oczywiste zafałszowanie danych przez Eddingtona i innych stanowi bezczelne pogwałcenie procesu naukowego, które wypaczało badania przez całą resztę stulecia.
McCausIand oświadczył, że "poufne oświadczenie o ostatecznym potwierdzeniu ogólnej teorii względności Einsteina z listopada 1919 roku nie było tryumfem nauki, jak jest często przedstawiane, ale jednym z najbardziej godnych pożałowania wydarzeń w historii dwudziestowiecznej nauki".
Mówi się, że Einstein nie znał wyników doświadczenia M-M. Jednak, znał.
Z kolei w liście do B. Jaffe Einstein napisał:
Nie ulega kwestii, iż doświadczenie Michelsona wywarło poważny wpływ na moją pracę w tym sensie, że wzmocniło moje przekonanie o słuszności zasad szczególnej teorii względności. Z drugiej zaś strony byłem dość mocno przekonany o słuszności tej zasady, nim dowiedziałem się o samym eksperymencie i jego wyniku. W każdym razie doświadczenie Michelsona rozwiało, praktycznie biorąc, wszelkie wątpliwości, jeśli chodzi o słuszność tej zasady w optyce, i wykazało, że zasadnicza zmiana podstawowych pojęć fizyki jest nieunikniona.
15 stycznia 1931 roku w Pasadenie odbył się po konferencji naukowej bankiet z udziałem wielu uczonych z całego świata na cześć schorowanego już Michelsona, podczas którego Einstein publicznie w obecności wielu wybitnych fizyków, między innymi R. Millikana i G. Hale, wygłosił krótką mowę i w pewnym momencie tymi słowy zwrócił się do Michelsona:
Pan, czcigodny doktorze Michelson, rozpoczął tę pracę, kiedy byłem dzieckiem i nie miałem nawet trzech stóp wzrostu. To pan poprowadził fizyków na nowe drogi i swoją wspaniałą pracą eksperymentalną utorował drogę rozwojowi teorii względności. Odkrył pan podstępny błąd w ówczesnej teorii eteru, stwarzając bodziec dla Lorentza i Fitzgeralda, z ich zaś pomysłów wyrosła szczególna teoria względności. Bez pańskich prac ta teoria byłaby dzisiaj zaledwie interesującą spekulacją; to pańskie pomiary pierwsze oparły ją na realnej podstawie.
Słowa te Michelsona głęboko wzruszyły, wstał i bardzo podziękował za uznanie zarówno w imieniu własnym jak i nieżyjącego już od siedmiu lat Morleya.
Sam Michelson w swojej książce Studies in Optics opublikowanej w 1927 r. stwierdził, że teoria względności musi zostać zaakceptowana przez wszystkich, chociaż początkowo nie należał do jej gorących entuzjastów.
The Greatest Hoax in 20th Century Science
By Richard Moody Jr.
http://blog.hasslberger.com/Moody%20-Eclipse_Data_From_1919.pdf
Einstein był zagorzałym wyznawcą poglądu o niezmiennym i nieskończonym Wszechświecie. Według Hipotezy Stanu Stacjonarnego Wszechświat wygląda tak samo z każdej pozycji przestrzeni. Jest jednorodny. Nie miałby on początku ani końca, istniałby tu zawsze i tak samo wyglądał.
Einstein, w swoim ograniczonym widzeniu Wszechświata, zakładając naiwnie jego statyczny charakter (tzn. nierozszerzający i niezapadający się), m. inn: na bazie stałej kosmologicznej Λ, stworzył swoją OTW, i tym samym porwał się z motyką na Słońce.
Jednakże odkrycie rozszerzającego się Wszechświata zakwestionowało wprowadzenie tej stałej, jak również samej konstrukcji teorii względności.
W sumie powstał sztuczny twór a stworzona teoria okazała się niepowodzeniem z dwóch powodów: statyczny Wszechświat opisywany przez tą teorię byłby niestabilny, co więcej, obserwacje prowadzone przez Huble’a pokazały, że nasz Wszechświat nie jest statyczny, ale się rozszerza.
Lemaitre odkrył, że model Wszechświata wynikajacy z równań Einsteina jest dynamiczny, nie statyczny. Nietrudno sie o tym przekonać. Skoro wszystkie obiekty w kosmosie wzajemnie się przyciagają, to w końcu muszą zgromadzić się w jednym miejscu i w konsekwencji cała masa Wszechświata spocznie na dnie ogromnego czasoprzestrzennego dołu. Z takiego rozumowania wynika że Wszechświat nie może być statyczny.
Aby naprawić sytuację, wprowadził on dodatkowe założenia, z których wynika że między galaktykami działa nowy rodzaj siły.
Dodał do swoich równań człon, który był czymś w rodzaju niewielkiej siły odpychającej, równoważącej grawitacyjne przyciąganie materii, w rezultacie czego Wszechświat pozostawał statyczny.
Siły te nazwano siłami odpychania kosmicznego, a człon równania stałą kosmologiczną.
Lemaitre natomiast nie widział powodu, by wprowadzać stałą kosmologiczną, ot tak sobie, wziętą z sufitu.
Pozostał więc przy modelu rozszerzającego się Wszechświata.
Model Wszechświata stacjonarnego Einsteina współczesna nauka traktuje jako nieaktualny, przypisując mu wartość jedynie historyczną. Ale wielu fizyków udaje, że tego nie widzi, zachwycają się OTW i mówią, że przyszłość pokaże, że to właśnie Einstein był najbliższy prawdy.
Według zasady Macha bezwładność materii (opór przy przyspieszaniu) nie wynika z własności wewnętrznej materii, ale stanowi miarę jej oddziaływania z całym Wszechświatem.
Bezwładność ta występuje tylko, dlatego, że istnieje pozostała materia we Wszechświecie.
Zasada ta, jako hipoteza została sformułowana przez fizyka i filozofa Ernsta Macha.
Była jedną z inspiracji Alberta Einsteina przy tworzeniu ogólnej teorii względności (OTW), a ostatecznie okazała się z nią sprzeczna.
Ja, osobiście mam przekonanie do zasady Macha a tym samym jest to kolejny mój powód na nie zaakceptowanie OTW.
Warto przypomnieć jak sam Einstein już po wielu latach oceniał swoją teorię względności, wątpiąc w to co sam stworzył.
Popatrzmy! Cytat z "Subtle is the Lord. The science and the life of Albert Einstein", Abraham Pais, str. 467:
" Teoria względności i teoria kwantów ... wydają się nie przystosowane do połączenia się w jedną zunifikowana teorię... te dwa koniki biegną nieuchronnie w przeciwnych kierunkach .... Nawet ja sam nie mogę polegać z cała pewnością na moim .... zakładam jako całkiem możliwe, że fizyki nie da się oprzeć na pojęciu pola t.j. na strukturach ciągłych. O ile tak jest wtedy nie zostaje absolutnie nic ze zbudowanego przeze mnie gmachu, włączając w to teorię grawitacji....
A w innym miejscu ten sam A. Einstein:
Jak długo rzeczywistość opiera się na matematyce, nie można być pewnym tego, że ona opiera się na rzeczywistości.
A co o pracy Einsteina powiedział Nicola Tesla:
Myślę, że obiekty materialne nie przyciągają się wzajemnie ale eter sprawia, że obiekt materialny napiera na inny. Błędnie nazywamy to zjawisko grawitacją.
Mówi się, że grawitacyjna czasoprzestrzeń wg OTW A. Einsteina, takie „coś”
a może nawet taką poniższą już „trąbę” przypomina.
To jest jakiś dziwoląg, co to jest i komu to jest potrzebne, to ja nie wiem.
I ja mam to kupić, by nie powiedzieć łyknąć?
Reasumując: STW oparta na odrzuceniu eteru Ziemi i założeniu stałości prędkości światła, nie względem tegoż eteru Ziemi, a względem wszystkich innych poruszających się wolniej czy szybciej układów, jest krzywym zwierciadłem nadającym się jedynie do kabiny śmiechu.
Kiedyś, jak byłem małym chłopakiem, to w takiej kabinie śmiechu nawet byłem i widziałem w krzywym zwierciadle swój zdeformowany obraz.
I było to takie nawet wesołe i do śmiechu. Ale przeglądać się można było i każdy siebie nawet rozpoznawał.
An Introduction to the Meaning and Structure of Physics by Leon N. Cooper
Tutaj mamy do jednak do czynienia z układem kinematycznym, no i na dodatek ten obrót wokół osi.
Jest to bardzo małe przesunięcie czasowe.
Ramiona interferometru w obydwu położeniach dawały tą samą ostrość prążków. Ku zaskoczeniu nie wykryto ruchu prążków.
Wynik doświadczenia był zdumiewający dla ówczesnych fizyków; powszechnie wątpiono w prawdziwość i dokładność pomiaru.
A prawda jest taka, że tak małej wartości, 2,4*10^-6 / 3*10^-5 = 0,08 długości fali, na dodatek, przy zakłóceniach przy obrocie, nie da się wyłapać. Na dodatek, jest to metoda pomiaru, niby taka sama ale i pogłębiona o obrót. A ten obrót na pewno gubi dokładność. Gubi te 2,4*10^-6 / 3*10^-5 = 0,08 długości fali
Tu się rozbija o dokładność. Czy fizycy złapią kiedykolwiek te 0,08 długości fali?
Wg mnie trzeba zmienić metodę.
*I to jest jedna możliwa przyczyna, że nic nie zaobserwowano.
*Druga przyczyna mogła być obecność eteru Ziemi, który z nią się porusza.
Tutaj mamy do jednak do czynienia z układem kinematycznym, no i ten obrót wokół osi. Żeby cokolwiek powiedzieć, trzeba było sprawdzić, czy idea pomiaru w ogóle działa. Ponieważ, takiej możliwości ta metoda nie daje, nie sprawdzono wstępnie, czy ta metoda, w ogóle, działa.
Dla ramienia wg pierwszego doświadczenia Michelsona L = 60 cm, V = 3*10^6 cm/s i c = 3*10^10 cm/s
różnica ta jest równa w przybliżeniu
W kierunku wzdłużnym czas przelotu tak samo jak wg Michelsona
Trównol = T1 + T2 = L/(c-V) + L/(c+V) = 2L/c * (1+V^2/c^2)
W kierunku poprzecznym czas przelotu wg Potiera i Lorentza
Tprostop = 2L/c *(1 +V^2/2c^2)
Obrót interferometru sprawia, że to ramie, które było pierwotnie prostopadłe do kierunku ruchu, przyjmuje teraz położenie równoległe. Wtedy przesunięcie prążka interferencyjnego obliczana z różnicy między Trównol i Tprostop, po pomnożeniu przez dwa bo obrót ramion podwaja różnicę, będzie:
ΔT = 2 x [Trównol – Tprostop ] = 2 * ΔT’ = 2(Trównol – Tprostop)
ΔT = 2[2L/c * (1+V2/c2) - 2L/c *(1 +V^2/2c^2)] = 2*2*L/c * V^2/c^2
ΔT = 2 x [Trównol –Tprostop ] = 4*L/c * V^2/c^2
Dla ramienia
L = 600 cm, V = 3*10^6 cm/s i c = 3*10^10 cm/s
różnica ta jest równa w przybliżeniu
ΔT = 2 x [Trównol –Tprostop ] = 4*10^-16 s.
Jest to przesunięcie czasowe pięciokrotnie większe niż dla wersji pierwszej Michelsona.
Analogicznie jak przy pierwszym eksperymencie Michelsona, przy długości fali światła widzialnego 3*10^-5 cm, spowodowana obrotem interferometru zmiana czasów przelotu obu sygnałów odpowiada przestrzennemu przesunięciu tych sygnałów na odległość:
Rzeczywista zaobserwowana wartość była zdecydowanie mniejsza niż dwudziesta część tego, a prawdopodobnie nawet mniej niż czterdziesta część.
Michelson, 1881
http://en.wikisource.org/wiki/The_Relative_Motion_of_the_Earth_and_the_Luminiferous_Ether
http://en.wikisource.org/wiki/On_the_Relative_Motion_of_the_Earth_and_the_Luminiferous_Ether
Literatura:
Albert Einstein do późnego dzieciństwa miał trudności z wyrażaniem się. Pierwszy raz zetknął się z nauką, gdy miał pięć lat. Jego ojciec pokazał mu kompas, którego działania na odległość wywarło na nim głębokie wrażenie, wydawało mu się „cudowne” i bardzo go zaskoczyło.
Rodzice Einsteina byli niepraktykującymi Żydami, ale krewny uczył Alberta elementów judaizmu. Około jedenastego roku życia przeszedł przez fazę bardzo religijną, komponując pieśni religijne, które śpiewał w drodze do szkoły. „Ale po przeczytaniu pierwszych książek naukowych – jak powiedział młody Albert - skończyłem z wiarą Abrahama»
W wieku dwunastu lat niewielka książeczka o euklidesowej geometrii, którą później nazwał „świętą księgą geometrii”, wywarła na nim silne wrażenie („jasność i pewność dowodów wywarła na nim nieopisane wrażenie na mnie"). Wujek Jakub, zastępca inżyniera w firmie ojca zajmującej się sprzętem elektrycznym, zadawał mu problemy matematyczne.
Max Talmey, student medycyny, który często jadał obiady z Einsteinami, proponował mu książki naukowe i późniejsze dzieła Kanta, po czym często prowadzili długie dyskusje. Od dwunastego do szesnastego roku życia uczył się rachunku różniczkowego i całkowego.
Einstein miał stosunkowo nietypowe wykształcenie w porównaniu z wybitnymi naukowcami, którzy byli mu później rówieśnicy. Naukę rozpoczął w gimnazjum Luitpold w Monachium. Od najmłodszych lat celował w fizyce i matematyce i wkrótce zdobył wiedzę matematyczną, którą zwykle można uzyskać jedynie u dziecka kilka lat od niego starszego. Zaczął uczyć się algebry, rachunku różniczkowego i geometrii euklidesowej w wieku dwunastu lat; poczynił tak szybkie postępy, że jeszcze przed trzynastymi urodzinami odkrył oryginalny dowód twierdzenia Pitagorasa. Nauczyciel rodzinny, Max Talmud, powiedział, że zaledwie krótki czas po tym, jak dał dwunastoletniemu Einsteinowi podręcznik do geometrii, chłopiec przestudiował całą książkę. Następnie poświęcił się wyższej matematyce. Wkrótce lot jego matematycznego geniuszu był tak wysoki, że nie mogłem nadążać. Jego miłość do algebry i geometrii była tak wielka, że już w wieku dwunastu lat był przekonany, że naturę można rozumieć jako „strukturę matematyczną”.
W
wieku trzynastu lat, kiedy zakres jego entuzjazmów poszerzył się o
muzykę i filozofię, Einstein zetknął się z Krytyką czystego
rozumu Kanta. Kant stał się jego ulubionym filozofem; według jego
wychowawcy: „Był wtedy jeszcze dzieckiem, miał zaledwie
trzynaście lat, a mimo to dzieła Kanta, niezrozumiałe dla zwykłych
śmiertelników, wydawały mu się jasne”. Einstein odnotował, że
„opanował rachunek całkowy i różniczkowy ” mając zaledwie
czternaście lat.
Einstein, wówczas piętnastoletni,
pozostał w Monachium, aby dokończyć naukę. Jego ojciec chciał,
żeby studiował elektrotechnikę, ale był uczniem, któremu reżim
i metody nauczania w gimnazjum nie odpowiadały. Młody
chłopiec już na początku buntuje się przeciwko arbitralnej władzy
nauczycieli, dlatego często jest przez nich przedstawiany jako
element zły, bardzo bezmyślny. Później napisał, że
stosowana przez szkołę polityka ścisłego uczenia się na pamięć
jest szkodliwa dla kreatywności. Według Marii Einstein jej
brat podczas nauki w gimnazjum Luitpold stał się nerwowy. Pojawiły
się nawet objawy depresji.
Gdy
miał 15 lat (grudzień 1894 r.) został wydalony z gimnazjum
Luitpold (jego grecki nauczyciel uznał jego obecność za niezgodną
z panującą tam wówczas surową dyscypliną). Miał doskonałe
wyniki tylko z matematyki i fizyki.
W 1895 r. dołączył do
rodziców w Pawii we Włoszech i zrzekł się obywatelstwa
niemieckiego (porzucenie to zostało sformalizowane w 1896 r.). We
wniosku o wyrzeczenie się obywatelstwa niemieckiego oświadczył, że
nie wyznaje żadnego wyznania, podpisując tym samym swoje oficjalne
zerwanie z religią żydowską.
Będąc we Włoszech jako
nastolatek napisał esej zatytułowany „O badaniu stanu eteru w
polu magnetycznym”.
Einstein w wieku 16 lat (ok. 1895) rozważał
ważny eksperyment myślowy. Wspomniał o tym publicznie po raz
pierwszy ponad pół wieku później, w swoich Notach
autobiograficznych z 1946. Młody Albert zastanawiał się, co
by się działo przy ruchu z prędkością światła. Wówczas fala
elektromagnetyczna taka jak światło, stałyby nieruchomo w miejscu,
nie wykazując żadnego ruchu. Ale, wg Einsteina, przeczyło to, jak i ... równaniom Maxwella.
W wieku 16 lat zdecydował
się dołączyć do Szwajcarskiego Federalnego Instytutu Technologii
w Zurychu (ETHZ), do którego można wówczas uzyskać dostęp bez
matury. Próba zdania egzaminu zakończyła się niepowodzeniem.
Powodem były słabe wyniki egzaminów z przedmiotów
humanistycznych.
Za radą dyrektora ETHZ Einstein postanowił
spędzić rok w Aarau w Szwajcarii, by ukończyć szkołę
średnią.
Tam zastał bardziej otwartą i sprzyjającą atmosferę
do nauki, a uczniów zachęcano bardziej do samodzielnego myślenia
niż do pamięciowego uczenia przedmiotów humanistycznych.
We
wrześniu 1896 r. zdał tam maturę. Matura (zaliczenie szkoły
średniej) przyznana mu we wrześniu tego roku potwierdziła,
że dobrze radził sobie z większością programu nauczania,
przyznając mu najwyższą ocenę 6 z historii, fizyki i algebry i geometrii. W wieku siedemnastu lat rozpoczął
czteroletnie studia dyplomowe z nauczania matematyki i fizyki w
Federalnej Szkole Politechnicznej.
W tym samym roku zrzekł się
obywatelstwa niemieckiego. Zrobił to w celu
uniknięcia służby wojskowej i na znak protestu przeciwko
nastrojom militarnym panującym wówczas w Niemczech.
W 1896 bez
przynależności państwowej zdał egzamin i jesienią wstąpił do
ETHZ, gdzie zaprzyjaźnił się z matematykiem Marcelem Grossmannem,
który później pomagał mu w geometrii nieeuklidesowej. Dyplom
uzyskał z trudem w 1900 r., przyznając w swojej autobiografii, że
„nie potrafi śledzić zajęć, robić notatek i pracować nad nimi
naukowo”.
W tym okresie pogłębiał swoją wiedzę jako samouk, czytając podręczniki, m.in. Kirchhoffa, Hertza, Helmholtza i
Maxwella. Jego przyjaciel Michele Besso zapoznał go z ideami
Mechaniki Ernsta Macha .
21 lutego 1901 r. Einstein przyjął
obywatelstwo szwajcarskie, które zachował do końca życia. Mając
już dyplom wykładowcy nauk ścisłych, zaczął szukać pracy. Starał się bezskutecznie o asystenturę u wykładającego w ETHZ
Webera, a później u Hurwitza i Wilhelma Ostwalda. Dopiero w maju
1901 r. został zatrudniony na krótko jako zastępca nauczyciela w
szkole średniej w Winterthur w Szwajcarii. W tym czasie zajmował
się tam ruchem materii względem eteru i kinetyczną teorią gazów.
Od października 1901 r. do stycznia 1902 r. uczył w prywatnej
szkole w Schaffhausen a równolegle pracował nad swoją pracą
doktorską dotyczącą kinetycznej teorii gazów.
Ostatecznie
Albert rezygnuje z odejścia od środowiska akademickiego i
znalezienia pracy w administracji. W lutym 1902 r. przeprowadził się
do Berna, gdyż spodziewał się dostać stałą pracę w
Szwajcarskim Urzędzie Patentowym w Bernie. Utrzymywał się z
udzielania korepetycji. W czerwcu został zatrudniony na okres próbny
jako ekspert techniczny trzeciej klasy w urzędzie patentowym a trzy
miesiące później zatrudniono go na stałe.
Autor: Nikola Tesla
Uniwersalne prawa nigdy wcześniej nie ujawnione: sekrety Keely'ego - zrozumienie i wykorzystanie nauki o wibracji współczulnej Sto lat temu naukowiec/wynalazca/filozof John Keely zbudował różne urządzenia, które były w stanie pokonać grawitację, tunelować przez skały za pomocą ręcznego urządzenia, wykorzystywać akustykę do zasilania silników i tworzyć nadprzewodnictwo za pomocą drutów wykonanych ze złota, srebra i platyny. Prawie zagubiona, ta książka w końcu kompiluje dziesięć lat badań redaktora / autora, które wyjaśniają zastosowaną technologię. Zrozumiałe dla laika i przydatne dla najbardziej zaawansowanego badacza. Fizyka wibracji współczulnych jest zjednoczeniem wielu różnych dyscyplin naukowych, inżynieryjnych i filozoficznych w nowy paradygmat. Ta nauka pokazuje podobieństwo, które leży u podstaw wszystkich zjawisk - wibracji! "Sympatyczna siła wibracyjna odkryta przez Keely'ego będzie wystarczająca, aby uczynić go największym odkrywcą tej epoki." – H.P. Bławatska, The Secret Doctrine, 1888 |



















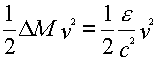







,+prawid%C5%82owy+czas+dla+poprzecznego+przelotu.jpg)
,+prawid%C5%82owy+czas+dla+poprz.+przelotu.jpg)


Brak komentarzy:
Prześlij komentarz